b.stefanuk.ca

Appearance

Binary Tree Traversal ​

binary-tree-traversal

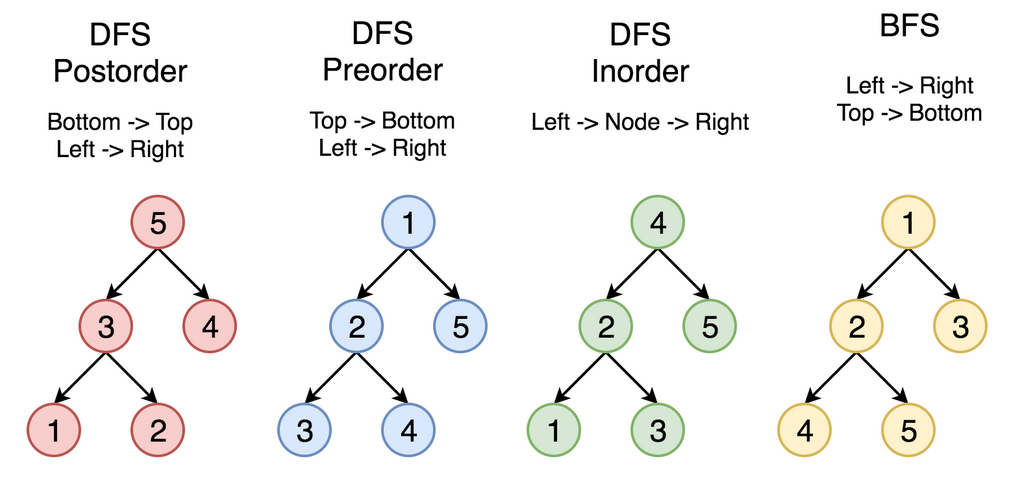
Breadth First Search (BFS) ​

BFS is also known a Level-order Traversal as it moves through each level of the tree, before moving to the next. This is typically best to code with a queue, in which each node is considered, and if it has left of right nodes, then those are added to the queue.

python
def bfs_recursive1(root):
    node = root
	queue = deque() # Could also use a list here
	result = []
	queue.append(node)
	while len(queue) > 0:
		node = queue.popleft()
		result.append(node.val)
		if node.left:
			queue.append(node.left)
		if node.right:
			queue.append(node.right)
	return result
#out: [1,2,3,4,5,6,7,...]

def bfs_recursive2(root):
    node = root
	queue = deque() # Could also use a list here
	next_queue = deque()
	result = []
	queue.append(node)
	while len(queue) > 0:
		result.append([node.val for node in queue])
		for node in queue:
			if node.left:
				next_queue.append(node.left)
			if node.right:
				next_queue.append(node.right)
		queue = next_queue
		next_queue = []
	return results
#out: [[1], [2,3], [4,5,6,7],...]
def bfs_recursive1(root):
    node = root
	queue = deque() # Could also use a list here
	result = []
	queue.append(node)
	while len(queue) > 0:
		node = queue.popleft()
		result.append(node.val)
		if node.left:
			queue.append(node.left)
		if node.right:
			queue.append(node.right)
	return result
#out: [1,2,3,4,5,6,7,...]

def bfs_recursive2(root):
    node = root
	queue = deque() # Could also use a list here
	next_queue = deque()
	result = []
	queue.append(node)
	while len(queue) > 0:
		result.append([node.val for node in queue])
		for node in queue:
			if node.left:
				next_queue.append(node.left)
			if node.right:
				next_queue.append(node.right)
		queue = next_queue
		next_queue = []
	return results
#out: [[1], [2,3], [4,5,6,7],...]

Depth First Search (DFS) ​

DFS searches all the way down a branch before moving to the next branch. There are three ways to search with DFS, which depend mainly on when the item is added to the results

Pre-order Traversal ​

Pre-order traversal adds elements to its search output before checking to see whether there are left or right nodes.

python
def dfs_preorder_recursive1(root):
	results = []
	def traverse(node):
		results.append(node)
		if node.left:
			traverse(node.left)
		if node.right:
			traverse(node.right)
	traverse(root)
	return results

def dfs_preorder_recursive2(root):
	results = []
	def traverse(node):
		if node:
			results.append(node.val)
			traverse(node.left)
			traverse(node.right)
	traverse(root)
	return results

def dfs_preorder_iterative1(root):
    node = root
    stack = deque()
    results = []
    stack.append(node)
    while len(stack) > 0:
        if node is not None:
            results.append(node.val)
            stack.append(node)
            node = node.left
        else:
            node = stack.pop()
            node = node.right
    return results

def dfs_preorder_iterative2(root):
    node = root
    stack = deque()
    results = []
    stack.append(node)
    while len(stack) > 0:
        node = stack.pop()
        results.append(node.val)
        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)
    return results
def dfs_preorder_recursive1(root):
	results = []
	def traverse(node):
		results.append(node)
		if node.left:
			traverse(node.left)
		if node.right:
			traverse(node.right)
	traverse(root)
	return results

def dfs_preorder_recursive2(root):
	results = []
	def traverse(node):
		if node:
			results.append(node.val)
			traverse(node.left)
			traverse(node.right)
	traverse(root)
	return results

def dfs_preorder_iterative1(root):
    node = root
    stack = deque()
    results = []
    stack.append(node)
    while len(stack) > 0:
        if node is not None:
            results.append(node.val)
            stack.append(node)
            node = node.left
        else:
            node = stack.pop()
            node = node.right
    return results

def dfs_preorder_iterative2(root):
    node = root
    stack = deque()
    results = []
    stack.append(node)
    while len(stack) > 0:
        node = stack.pop()
        results.append(node.val)
        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)
    return results

In-order Traversal ​

In-order traversal adds elements to its search output after checking if it has a left node but before checking for a right node.

python
def dfs_inorder_recursive(root):
	results = []
	def traverse(node):
		if node.left:
			traverse(node.left)
		results.append(node)
		if node.right:
			traverse(node.right)
	traverse(root)
	return results

def dfs_inorder_recursive2(root):
	results = []
	def traverse(node):
		if node:
			traverse(node.left)
			results.append(node.val)
			traverse(node.right)
	traverse(root)
	return results

def dfs_inorder_iterative1(root):
    node = root
    stack = deque()
    results = []
    stack.append(node)
    while len(stack) > 0:
        if node is not None:
            stack.append(node)
            node = node.left
        else:
            node = stack.pop()
            results.append(node.val)
            node = node.right
    return results[:len(results)-1]
def dfs_inorder_recursive(root):
	results = []
	def traverse(node):
		if node.left:
			traverse(node.left)
		results.append(node)
		if node.right:
			traverse(node.right)
	traverse(root)
	return results

def dfs_inorder_recursive2(root):
	results = []
	def traverse(node):
		if node:
			traverse(node.left)
			results.append(node.val)
			traverse(node.right)
	traverse(root)
	return results

def dfs_inorder_iterative1(root):
    node = root
    stack = deque()
    results = []
    stack.append(node)
    while len(stack) > 0:
        if node is not None:
            stack.append(node)
            node = node.left
        else:
            node = stack.pop()
            results.append(node.val)
            node = node.right
    return results[:len(results)-1]

Post-order Traversal ​

https://leetcode.com/problems/binary-tree-postorder-traversal/discuss/45648/three-ways-of-iterative-postorder-traversing-easy-explanation

Post-order traversal adds elements to its search output after checking for the existence of either its left and right nodes.

python
def dfs_inorder_recursive(root):
	results = []
	def traverse(node):
		if node.left:
			traverse(node.left)
		if node.right:
			traverse(node.right)
		results.append(node)
	traverse(root)
	return results

def dfs_inorder_recursive2(root):
	results = []
	def traverse(node):
		if node:
			traverse(node.left)
			traverse(node.right)
			results.append(node.val)
	traverse(root)
	return results

def dfs_postorder_iterative1(root):
    node = root
    stack = deque()
    results = []
    stack.append(node)
    while len(stack) > 0:
        node = stack.pop()
        results.append(node.val)
        if node.left:
            stack.append(node.left)
        if node.right:
            stack.append(node.right)
    out = []
    while results:
        out.append(results.pop())
    return out
def dfs_inorder_recursive(root):
	results = []
	def traverse(node):
		if node.left:
			traverse(node.left)
		if node.right:
			traverse(node.right)
		results.append(node)
	traverse(root)
	return results

def dfs_inorder_recursive2(root):
	results = []
	def traverse(node):
		if node:
			traverse(node.left)
			traverse(node.right)
			results.append(node.val)
	traverse(root)
	return results

def dfs_postorder_iterative1(root):
    node = root
    stack = deque()
    results = []
    stack.append(node)
    while len(stack) > 0:
        node = stack.pop()
        results.append(node.val)
        if node.left:
            stack.append(node.left)
        if node.right:
            stack.append(node.right)
    out = []
    while results:
        out.append(results.pop())
    return out